Содержание
как легко и просто запомнить?» — Яндекс Кью
Популярное
Сообщества
Сигналы регулировщикаСигналы регулировщика память
Анонимный вопрос
·
134,3 K
ОтветитьУточнить
Первый
Даниил Магомедов
57
Инженер широкого кругозора · 19 апр 2018
Нужно запомнить всего три «нельзя».
Если регулировщик стоит к вам спиной — ехать нельзя.
Если жезл поднят — ехать нельзя.
При всех остальных сигналах, представим, что жезл — это шлагбаум! Нельзя ехать в направлении, которое он закрывает.
43,6 K
Ярослав Окурков
27 ноября 2019
Тут всего 2 нельзя
Комментировать ответ…Комментировать…
Первый
Vladimir S.
3
18 сент 2021
Если палка смотрит вверх, значит время для потех.
Если палка смотрит в рот, делай правый поворот.
Если палка смотрит влево, ты на трассе королева.
Если палка смотрит вправо, ехать не имеешь права.
Грудь к тебе или спина — для водителей стена.
Если боком стоит «браво» можно прямо иль направо. Читать далее
Комментировать ответ…Комментировать…
Александр Евгеньевич
2
22 сент 2020
Можно запомнить с помощью стишка в одном из ответов =)
Я лично не зазубривал, а именно разобрался, в плане жестов и сигналов регулировщика по видео с ютуба https://youtu.be/RNEWl1dveps
Гляньте. Думаю после просмотра, проблем с пониманием жестов и сигналов регулировщика у вас не возникнет! Удачи на дорогах
Комментировать ответ…Комментировать…
Первый
Владимир П.
318
7 июл 2019
Палка вверх устремлена — всем стоять велит она.
Если палка смотрит в рот, делай правый поворот.
Если палка смотрит влево, ты на трассе королева (разрешён проезд в любом направлении).
Если палка смотрит вправо, ехать не имеешь права.
Грудь к тебе или спина — для водителей стена.
Если боком стоит «браво» можно прямо иль направо. Читать далее
109,1 K
Равик
16 января 2020
Осталось сочинить музыку и будет новый мюзикл…эротический.
А теперь правильный ответ.
Движение РАЗРЕШЕНО — из… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
1 ответ скрыто(Почему?)
Сигналы регулировщика: что означают, как запомнить
Автор:
Алексей Кокорин
Мы уже вспоминали, что будет, если нарушать указания регулировщиков, которых мы видим на дорогах довольно редко. Сегодня же давайте поговорим об их ключевой функции – собственно регулировании движения. Что означают жесты, как их запомнить и можно ли выжить в современном городе, не зная сигналов регулировщика?
Кто такой регулировщик и как он выглядит?
Для начала кратко вспомним, кто такой регулировщик. Стоит учитывать, что согласно ПДД регулировщиками могут быть не только сотрудники полиции, но также уполномоченные лица из числа работников подразделений транспортной безопасности, работники дорожно-эксплуатационных служб и дежурные на железнодорожных переездах и паромных переправах. Единственное условие – регулировщик должен быть в форменной одежде и (или) иметь отличительный знак и экипировку. То есть дорожный рабочий в оранжевом жилете и с жезлом, регулирующий движение на ремонтируемом участке дороги, – это тоже регулировщик, и согласно пункту 1.3 ПДД водители обязаны выполнять его распоряжения. А вот само наличие у регулировщика жезла или диска с красным сигналом возможно, но необязательно – правила говорят, что он «может применять их для лучшей видимости сигналов».
Единственное условие – регулировщик должен быть в форменной одежде и (или) иметь отличительный знак и экипировку. То есть дорожный рабочий в оранжевом жилете и с жезлом, регулирующий движение на ремонтируемом участке дороги, – это тоже регулировщик, и согласно пункту 1.3 ПДД водители обязаны выполнять его распоряжения. А вот само наличие у регулировщика жезла или диска с красным сигналом возможно, но необязательно – правила говорят, что он «может применять их для лучшей видимости сигналов».
Кроме сигналов стоит помнить о приоритете и полномочиях регулировщика. Самое важное здесь – то, что регулировщик имеет приоритет над всеми прочими средствами регулирования: пункт 6.15 ПДД гласит, что водители обязаны выполнять его указания, даже если они противоречат дорожным знакам, разметке и светофорам. Ну а пункт 2.4 ПДД указывает, что регулировщикам предоставлено право остановки транспортных средств.
Как разобраться в сигналах регулировщика?
В ПДД сигналы регулировщика изложены «от первого лица», и возможных поз здесь три: руки вытянуты в стороны или опущены; правая рука вытянута вперед; рука поднята вверх. Но мы для удобства рассмотрим варианты со стороны водителя легкового автомобиля, который может приближаться к регулировщику с четырех сторон. Кстати, тот же принцип лег в основу «народных правил», которые уже стали фольклором, так что вспомним заодно и их.
Но мы для удобства рассмотрим варианты со стороны водителя легкового автомобиля, который может приближаться к регулировщику с четырех сторон. Кстати, тот же принцип лег в основу «народных правил», которые уже стали фольклором, так что вспомним заодно и их.
Руки вытянуты в стороны или опущены
В этом случае водителям, приближающимся к регулировщику сбоку (справа или слева), разрешено ехать прямо и направо. Тем же, кто приближается спереди или сзади (со стороны груди и спины), движение запрещено. В народе это сформулировано так: «грудь и спина для водителя – стена».
Правая рука вытянута вперед
Здесь вариантов больше. Тем, кто приближается к регулировщику с его левого бока и видит руку, указывающую влево, можно ехать во всех направлениях (в фольклоре это звучит так: «если жезл смотрит влево – поезжай как королева»). Тем, кто приближается с правого бока и видит руку, указывающую вправо, движение запрещено («если жезл смотрит вправо – ехать не имеешь права»). То же самое касается приближения со спины – проезд также запрещен. Ну а тем, кто приближается со стороны груди, можно ехать только направо («если палка смотрит в рот – делай правый поворот»).
То же самое касается приближения со спины – проезд также запрещен. Ну а тем, кто приближается со стороны груди, можно ехать только направо («если палка смотрит в рот – делай правый поворот»).
Рука поднята вверх
Это самый простой вариант: если рука регулировщика поднята вверх, движение запрещено во всех направлениях.
Можно ли не запоминать сигналы регулировщика?
Вопрос сам по себе провокационный, и формальный ответ на него очевиден: нет, нельзя. Сигналы регулировщика – базовые основы ПДД, которые обязан знать каждый водитель. Однако в ПДД есть официальное «послабление» на этот счет: в правилах сказано, что «регулировщик может подавать жестами рук и другие сигналы, понятные водителям и пешеходам». То есть неопытным и забывчивым водителям, стоящим перед регулировщиком и создающим помехи для движения другим, регулировщик может подать более простые и очевидные сигналы о разрешенном направлении движения. Более того, во многих случаях регулировщики поступают так во всех случаях, направляя водителей жестами и взмахами рук.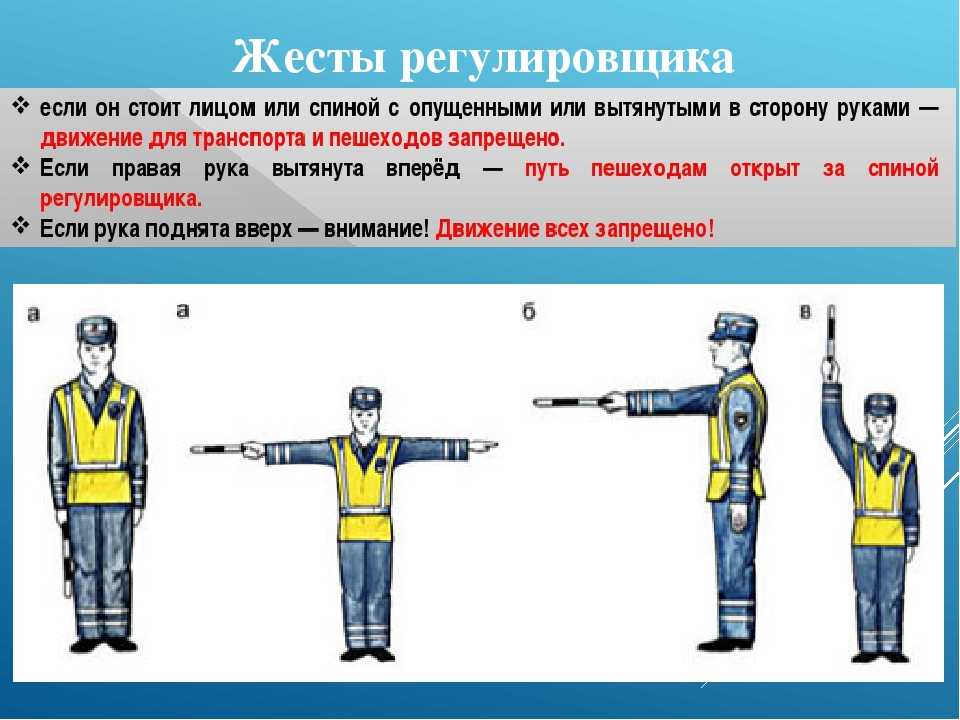 Однако стоит учитывать, что незнание сигналов, указанных в ПДД, не освобождает водителя, даже начинающего, от ответственности за несоблюдение указаний регулировщика. Так что сигналы стоит выучить обязательно, пусть в современных городах их не так часто можно встретить «в чистом виде».
Однако стоит учитывать, что незнание сигналов, указанных в ПДД, не освобождает водителя, даже начинающего, от ответственности за несоблюдение указаний регулировщика. Так что сигналы стоит выучить обязательно, пусть в современных городах их не так часто можно встретить «в чистом виде».
популярные вопросы
Новые статьи
Статьи / История
Праздник длиной в 45 лет: провожаем Ford Fiesta, вспоминая ее самые яркие достижения
Fiesta для компании Ford – практически такая же знаковая модель, как, к примеру, Golf для Volkswagen. Ведь за 45 с лишним лет произведено свыше 16 миллионов экземпляров семи поколений. Увы,…
586
3
0
03.12.2022
Статьи / Выставки
Нам на них ездить: новинки международной выставки автобусов Busworld 2022
С 29 ноября по 1 декабря в Москве проходила международная выставка автобусов Busworld 2022. Само собой, на этой выставке по понятным причинам не принимали участие MAN, Volvo, Scania и все ос…
Само собой, на этой выставке по понятным причинам не принимали участие MAN, Volvo, Scania и все ос…
1333
0
6
02.12.2022
Статьи / Практика
ATF, PSF и три разных цвета: что заливать в гидроусилитель и что можно смешивать
Про жидкость гидроусилителя руля, к сожалению, обычно вспоминают в двух случаях: когда насос уже умирает и начинает выть или если она куда-то вытекла. По-хорошему, конечно, её тоже надо меня…
1031
1
1
02.12.2022
Популярные тест-драйвы
Тест-драйвы / Тест-драйв
Haval Dargo против Mitsubishi Outlander: собака лает, чужестранец идет
В дилерском центре Haval на юге Москвы жизнь кипит: покупатели разглядывают машины, общаются с менеджерами и подписывают какие-то бумаги.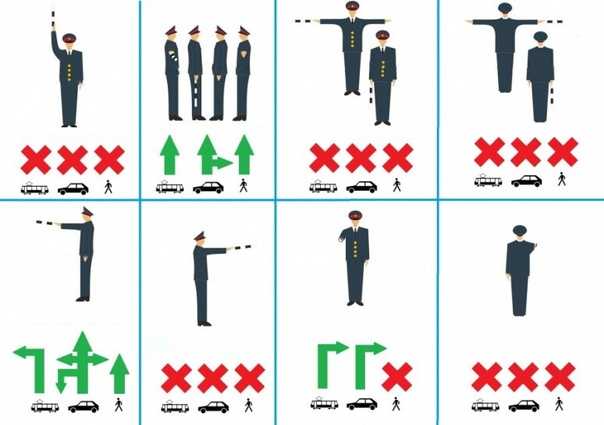 Пока я ждал выдачи тестового Dargo, такой же кроссов…
Пока я ждал выдачи тестового Dargo, такой же кроссов…
18046
7
205
13.09.2022
Тест-драйвы / Тест-драйв
Мотор от Mercedes, эмблема от Renault, сборка от Dacia: тест-драйв европейского Logan 1,0
Казалось бы, что нового можно рассказать про Renault Logan второго поколения, известный каждому российскому таксисту, что называется, вдоль и поперёк? Однако конкретно в этом автомобиле есть…
14486
10
41
13.08.2022
Тест-драйвы / Тест-драйв
Geely Coolray против Haval Jolion: бесплатный сыр? Если бы!
Хотите купить сегодня машину с полноценной гарантией, в кредит по адекватной ставке, без диких дилерских накруток? Сейчас это та еще задачка, ведь полноценную цепочку «представительство – з. ..
..
11707
26
30
10.08.2022
Объяснение точек удара хоккейной клюшки
Если вы не знакомы с термином точка удара или с тем, как он влияет на клюшки для хоккея на льду и на роликах, поход в профессиональный магазин, вероятно, оставит вас в недоумении. Вы увидите, что у каждого крупного производителя (CCM, True, Bauer, Warrior) есть по крайней мере две клюшки с разным видом, которые имеют одинаковую кривизну и жесткость. Единственное, что очевидно, это то, что художественные работы между ними очень разные.
У них разные точки удара
Точка удара — это термин, используемый в хоккейной индустрии для обозначения того, где клюшка должна сгибаться и отскакивать при стандартном приложении давления. Хоккейные клюшки состоят из множества слоев очень тонкого углеродного волокна, уложенных попеременно в разных направлениях, чтобы обеспечить максимальный щелчок и прочность при минимальном количестве материалов, чтобы снизить вес. То, как эти слои наносятся, придает жесткость и смягчает части стержня, чтобы управлять тем, где клюшка будет работать лучше всего. На изображениях ниже вы увидите точки удара, выделенные желтым цветом.
То, как эти слои наносятся, придает жесткость и смягчает части стержня, чтобы управлять тем, где клюшка будет работать лучше всего. На изображениях ниже вы увидите точки удара, выделенные желтым цветом.
Средняя точка удара
По умолчанию полностью однородная клюшка изгибается посередине при приложении давления. Это известно как клюшка для среднего удара и является наиболее распространенным стилем, используемым игроками НХЛ и ниже по всем направлениям. Они предназначены для помощи стрелкам, которые сильно наклоняются при броске, максимизируя передачу энергии, чтобы получить максимальную мощность при броске, сохраняя при этом высокую точность.
Некоторые примеры линий средней точки клюшки: Twig Rogue, CCM Tacks и Bauer Nexus.
Low Kick Point
Вторым по популярности стилем клюшек, используемым сегодня, является low-kick. Он спроектирован так, чтобы изгибаться в нижней точке (ближе ко льду) вдоль вала. Эта нижняя точка удара позволяет клюшке сгибаться, нагружаться и отпускать немного быстрее, чем конструкция со средним ударом. Кроме того, из-за более низкой точки удара на стержне не требуется полный вес игрока, чтобы максимизировать возможную скорость удара, поэтому он производит немного меньшую мощность при каждом ударе, чем клюшка со средней точкой удара.
Кроме того, из-за более низкой точки удара на стержне не требуется полный вес игрока, чтобы максимизировать возможную скорость удара, поэтому он производит немного меньшую мощность при каждом ударе, чем клюшка со средней точкой удара.
Вот некоторые примеры лоу-кик линий: Twig Dispatch, Warrior Covert, Bauer Vapor, Sher-wood Rekker и CCM RibCor.
Другие стили точек удара
Выше перечислены два наиболее распространенных стиля точек удара, используемых сегодня. Из-за возможности специализации в производстве хоккейных клюшек существует множество других доступных стилей ударных клюшек, которые используются реже и не производятся всеми производителями, но их полезно знать, поскольку они подходят для вашей игры.
Средняя-низкая точка удара
Это именно то, на что это похоже. Благодаря расположению точки удара между средней и нижней точками стержня клюшка загружается и отпускается немного быстрее, чем у модели со средним ударом, но немного медленнее, чем у модели с низким ударом. Генерируемая мощность будет больше, чем у лоу-кика, но все же ниже, чем у мид-кика.
Генерируемая мощность будет больше, чем у лоу-кика, но все же ниже, чем у мид-кика.
Линия клюшки Warrior Alpha — отличный пример средней и низкой точки удара.
High-Mid Kick Point
Опять же, именно так, как это звучит. Ударная точка изготавливается между средней и верхней точками вала. Такое расположение обеспечивает большую нагрузочную способность и максимальную передачу энергии по сравнению с другими стилями удара. Однако, как и во всех конструкциях, в целом, чем больше вырабатывается энергии, тем медленнее заряжается и высвобождается, а также увеличивается вероятность неточности выстрела.
Линия клюшки Bauer Supreme — наиболее часто встречающаяся версия этой сборки.
Переменная точка удара
Хоккейная клюшка с изменяемой точкой удара предназначена для изменения реакции в зависимости от положения руки вдоль стержня и места приложения веса. В идеале, это позволит быстро выпустить пулю, не жертвуя слишком большой силой выстрела.
CCM является основным производителем этой сборки со своей линейкой клюшек JetSpeed.
Какую точку удара выбрать?
На самом деле это зависит от того, как вы обычно играете в свою игру и хотите, чтобы ваша клюшка работала.
Средний удар ногой | Низкий удар |
| Больше мощности | Быстросъемный |
| Сбалансированное ощущение | Точность стрельбы |
| Универсальность | Чувство шайбы |
| Лучше всего подходит для мощной и точной стрельбы из различных положений. | Лучше всего подходит для игры вплотную к сетке и быстрых бросков |
Обязательно ознакомьтесь с другими материалами нашего блога, посвященными хоккею! И если вы еще этого не сделали, убедитесь, что вашей следующей палкой будет Twig.
Поделиться этой публикацией
пр.вероятность — Если сломать палку в двух точках, выбранных одинаково, вероятность того, что три полученные палочки образуют треугольник, равна 1/4.
 Есть хорошее доказательство этого?
Есть хорошее доказательство этого?
спросил
Изменено
6 лет, 4 месяца назад
Просмотрено
131 тысяч раз
$\begingroup$
Существует стандартная проблема элементарной вероятности, которая выглядит следующим образом. Рассмотрим палку длины 1. Выберите две случайные точки на палке и сломайте палку в этих точках. Какова вероятность того, что три полученных таким образом отрезка образуют треугольник?
Конечно, это вероятность того, что ни одна из коротких палочек не длиннее 1/2. Эта вероятность оказывается равной 1/4. См., например, задачу 5 в этих решениях домашних заданий.
Похоже, для этого ответа должен быть хороший аргумент, основанный на симметрии, но я не могу его понять. Я помню, как однажды видел решение этой проблемы, когда две конечные точки интервала соединялись в круг, но я не могу его реконструировать. Кто-нибудь может помочь?
Я помню, как однажды видел решение этой проблемы, когда две конечные точки интервала соединялись в круг, но я не могу его реконструировать. Кто-нибудь может помочь?
- пр.вероятность
- евклидова геометрия
$\endgroup$
4
$\begingroup$
Вот аргумент, который вы ищете (основанный на трюке, который Вендель использовал для вычисления вероятности того, что выпуклая оболочка набора случайных точек на сфере содержит центр сферы, который на самом деле является тот же скрытый вопрос):
Соедините концы палки в круг. Теперь представьте, что мы разрезаем в трех точках вместо двух. Мы можем образовать треугольник, если ни одна из получившихся частей не меньше 1/2, то есть если ни одна полуокружность не содержит все три наши точки разреза.
Теперь представьте, что разрез формируется в два этапа. На первом этапе мы выбираем три пары противоположных точек на окружности. Во втором мы выбираем одну точку из каждой пары для разрезания. Наборы из трех точек, лежащих в полуокружности (нетреугольники), точно соответствуют наборам из трех последовательных точек из шести выбранных нами точек. Это означает, что 6 из 8 возможных выборов на втором этапе приводят к нетреугольнику, независимо от пар точек, выбранных на первом этапе.
На первом этапе мы выбираем три пары противоположных точек на окружности. Во втором мы выбираем одну точку из каждой пары для разрезания. Наборы из трех точек, лежащих в полуокружности (нетреугольники), точно соответствуют наборам из трех последовательных точек из шести выбранных нами точек. Это означает, что 6 из 8 возможных выборов на втором этапе приводят к нетреугольнику, независимо от пар точек, выбранных на первом этапе.
$\endgroup$
2
$\begingroup$
Рассмотрим равносторонний треугольник с высотой 1. Нетрудно показать, что если вы случайно выберете точку в этом треугольнике, расстояния до трех сторон дадут то же самое распределение длин, которое вы получите, если сломаете палку в двух случайных точках. . Теперь геометрическое место точек, для которых ни одно расстояние не превышает 1/2, представляет собой меньший равносторонний треугольник, образованный соединением средних точек ребер, площадь которого составляет 1/4 площади исходного треугольника.
$\endgroup$
5
$\begingroup$
Треугольник возможен тогда и только тогда, когда ни одна часть не $>{1\over2}$. С вероятностью ${1\over2}$ оба разреза находятся по одну сторону от середины $M$, и в этом случае треугольник невозможен. Если разрезы $x$ и $y$,
$\ x < y$, лежат по разные стороны от $M$, то с вероятностью ${1\over 2}$ точка $x$ находится в своей половине левее, чем точка $y$ в правой половине. В этом случае треугольник также невозможен. Отсюда следует, что только ${1\over 4}$ всех разрезов допускают формирование треугольника.
$\endgroup$
1
$\begingroup$
Аргумент, который вы помните, звучит примерно так: если выбрать три точки на окружности, какова вероятность того, что они лежат в одной полуокружности?
Проблема обсуждается здесь:
http://godplaysdice. blogspot.com/2007/10/probabilities-on-circle.html
blogspot.com/2007/10/probabilities-on-circle.html
$\endgroup$
1
$\begingroup$
Да, вот хороший и красивый аргумент!
Сначала нужно нарисовать оси a и b . Вас просят равномерно выбрать точку в квадрате [0,1]x[0,1] . Теперь из-за симметрии (sic!) это эквивалентно выбору точек a и b равномерно в треугольнике, вырезанном из квадрата на b > a .
Таким образом, вы на самом деле равномерно выбираете точку внутри треугольника, определяемого линиями a>=0 , b<=1 , 'b>=a'.
Теперь найдем условия, при которых можно составить треугольник из коротких палочек. Мы должны иметь a + (1-b) > b-a , b-a + (1-b) > a и b > 1 - b , что действительно, как вы говорите, сводится к
b > 1/.2, а < 1/2, б-а < 1/2
Осталось заметить, что эти линии создают внутри большого треугольника маленький треугольник, похожий на большой, но со всеми длинами 1/2 от большого, поэтому площадь этого маленького треугольника равна ровно 1/4 площади оригинала!
$\endgroup$
4
$\begingroup$
Кажется естественным перефразировать вопрос в терминах барицентрических координат в треугольнике. Этими координатами являются числа $x$, $y$, $z$ из интервала $[0,1]$, удовлетворяющие уравнению $x+y+z=1$. Мы ищем тройки $(x,y,z)$ таких чисел, которые удовлетворяют трем неравенствам треугольника $x\le y+z$, $y\le x+z$ и $z\le x+y$. Заменив отношения «$\le$» на «$=$», мы получим отрезки, соединяющие середины ребер треугольника. Эти отрезки разрезают треугольник на четыре конгруэнтных подтреугольника. Центральный из этих четырех подтреугольников является областью, где выполняются все три неравенства треугольника, и эта область имеет площадь, равную одной четверти площади большого треугольника. {0.5} {2}{x}dx=\frac{1}{4}
{0.5} {2}{x}dx=\frac{1}{4}
$$
$\endgroup$
2
$\begingroup$
Вот как я объяснил это в своем блоге несколько лет назад, как шаг в решении связанной проблемы:
Если мы сломаем палку в двух случайных точках, $x$ и $y$, три получившихся куска имеют длины $x$, $(y - x)$ и $(1 - y)$, если $x$ находится слева от $y$
и $y$, $(x - y)$ , и $(1 - x)$, если $x$ находится справа от $y$
Три части образуют треугольник, если ни одна из частей не превышает половины длины палки. Другими словами, если
$(y > 1/2) И (x < 1/2) И (y - x) < 1/2$
, когда точка $x$ находится левее точки $y$ (первое изображение выше) и
$(x > 1/2) AND (y < 1/2) AND (x - y) < 1/2$
, когда $x$ находится справа от $y$ (второе изображение выше). Если мы построим все шесть из этих неравенств, мы получим площадь, которая представляет долю треугольников, образованных нашей сломанной палкой.
Заштрихованные области, представляющие условия, формирующие треугольник, в сумме составляют 1/4 общей площади, или вероятность образования треугольника равна 0,25.
$\endgroup$
2
$\begingroup$
Проблема действительно состоит в том, чтобы равномерно и случайным образом выбрать две точки $x,y$ на интервале $[0,1]$ так, чтобы длина каждого подинтервала была меньше $\frac{1}{2}$. Это эквивалентно вероятности того, что две точки, выбранные равномерно случайным образом на интервале $[0,1]$, попадают в интервал $[0,\frac{1}{2}]$, который равен $\frac{1}{2} \times\frac{1}{2}=\frac{1}{4}$.
Чтобы убедиться в этом, ясно, что одна точка, скажем, $x$, должна лежать в $[0,\frac{1}{2}]$, а другая, скажем, $y$, в $[\frac{ 1}{2},1]$. Теперь переместите $y$ назад на $\frac{1}{2}$ в точку $y'$. Теперь $y'
$\endgroup$
$\begingroup$
Пусть AB будет палкой.
WLOG мы можем предположить, что AB = 1 (поскольку вероятность не будет зависеть от длины AB).
Пусть палка сломана точками P и Q.
$AP=x$, $PQ=y$ и $QB=z$.
Поскольку $0\leq AP,PQ,QB \leq 1$, нам нужно рассмотреть все точки внутри куба $1\times 1\times 1 $.
Кроме того, точки лежат на плоскости x+y+z=1.
плоскость x+y+z=1(нажмите на ссылку, чтобы увидеть изображение плоскости)
О применении неравенств треугольника (т.е. $x+y>z,y+z>x\text{ и }x +z>y$) получаем, что чистая площадь точек, удовлетворяющих условию образования треугольника, есть заштрихованное зелье.
Заштрихованная область(Нажмите на ссылку, чтобы увидеть заштрихованную область)
Поскольку точки $J,K,I$ являются серединами сторон треугольника ACE. Вероятность = $\dfrac{\text{ Площадь }\Delta JKI}{\text{Площадь }\Delta ACE}=\dfrac{1}{4}$
Вероятность = $\dfrac{\text{ Площадь }\Delta JKI}{\text{Площадь }\Delta ACE}=\dfrac{1}{4}$
$\endgroup$
2
$\begingroup$
РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ ТОЛЬКО ОРИГИНАЛЬНОЙ ЛИНИИ:
Назовите конечные точки A и B, а середину M. Пусть N будет серединой MB. Назовем P первой случайной точкой, а Q — второй. В общем случае мы можем рассматривать точку P как лежащую между M и B. На AM пусть H будет точкой, для которой HP составляет половину длины исходной палки.
Чтобы 3 палочки образовали треугольник, необходимо и достаточно, чтобы общая длина любых 2 палочек была больше, чем у третьей. Следовательно, ни один кусок не может превышать половину длины исходной палки. Это немедленно говорит нам о том, что Q не может лежать на AH или PB, что немедленно исключает половину возможных точек для Q. Точно так же все точки на MP также исключаются.

 2, а < 1/2, б-а < 1/2
2, а < 1/2, б-а < 1/2